11.
Za dva kvadratna broja postoji jedan srednje proporcionalan broj i razmera kvadratnog broja prema kvadratnom je dva puta više od razmere strane prema strani.
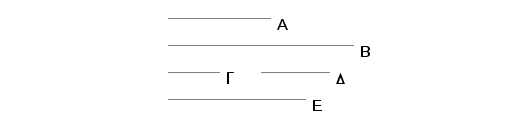
Neka su A i B dva kvadratna broja i strana A je G, a strana B i D. Tvrdim, da za brojeve A i B postoji jedan srednje proporcionalan broj i da je razmera A prema B dva puta viša od razmere G prema D.
Neka G, pomnoženo sa D, proizvodi E. Pošto je A kvadrat, a G je njegova strana, G pomnoženo samo sobom daje A. Iz istih razloga D pomnoženo samo sobom daje B. Pošto sad G pomnoženo svakim od brojeva G i D daje A odnosno E, biće G prema D, kao A prema E. Iz istih razloga je i G prema D kao E prema B. I prema tome je A prema E kao E prema B. Na ovaj način za dva broja A i B postoji srednje proporcionalan broj.
I tvrdim da je razmera A prema B dva puta viša od razmere G prema D. Zaista, pošto su tri broja A, E, B neprekidno proporcionalni, biće razmere A prema B dva puta više od A prema E. A ako se A odnosi prema E kao G prema D, biće razmera A prema B dva puta viša od razmere strane G prema strani D. A to je trebalo dokazati.