9.
Ako je jedan broj deo drugog broja, a treći broj isti deo četvrog broja, onda je i, posle permutacije, prvi broj isti deo ili isti delovi trećeg broja kao i drugi broj četrtog.
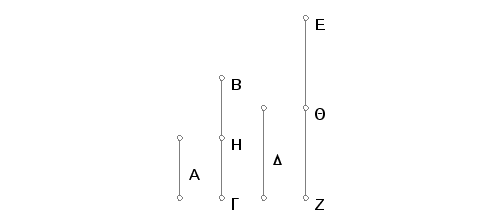
Naka je broj A onoliki deo broja BG koliki je deo broj D nekog broja EZ. Tvrdim da je, posle permutacije, A onoliki deo ili delovi broja D, koliki je deo ili delovi broj BG broja EZ.
Zaista, kako je A onoliki deo BG koliki je D deo EZ, to će i broj EZ sadržati onoliko brojeva jednakih D koliko broj BG sadrži brojeve jednakih A. Podelimo BG na delove BH i HG jednake A, a EZ na delove EQ, QZ jednake D. Na taj način je broj podelaka BH, HG jednak broju podelaka EQ, QZ.
I, ako su brrojevi BH, HG međusobno jednaki, biće i brojevi EQ i QZ međusobno jednaki, a i broj podelak BH, HG jednak broju podelaka EQ, QZ, te tako koliki deo ili kolike delove bude BH sačinjavao od EQ, isto toliki deo ili delove će sačinjavati i HG od QZ. Prema tome, koliki deo ili kolike delove bude BH sačinjavao od EQ, isto toliki deo ili tolike delove će sačinjavati i zbir BG od zbira EZ. No BH je jednako A, a EQ jednako D. Te tako, koliki deo ili kolike delove bude A sačinjavao od D, isto toliki deo ili delove sačinjavaće i BG od EZ. A to je trebalo dokazati.