Ako jedan broj čini iste delove drugog broja kao što umanjilac prvog broja čini delove umanjioca drugog broja, onda i ostatak prvog broja činin iste delove ostatka drugog broja.

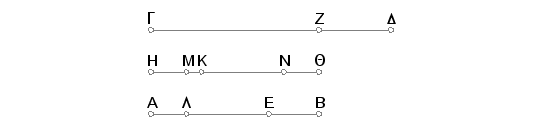
Neka broj AB čini iste delove broja GD ako što umanjilac AE čini delove umanjioca GZ. Tvrdim da i ostatak EB čini iste delove ostatka ZD kao i ceo broj AB celog broja GD.
Zaista, uzmimo HQ jednako AB. Tada kolike delove HQ čini od GD, tolike delove i AE čini od GZ. Podelimo HQ prema delovima GD na delove HK, KQ, a AE na delove AL i LE prema delovima GZ. Tada je broj podelaka HK, KQ jednak broju podelaka AL, LE. I pošto koliki HK bude bio deo od GD, toliki će i AL biti deo od GZ; a kako je GD veće od GZ, biće i HK veće od AL. Konstruišimo HM jednako AL. Onda, koliki HK bude bio deo od GD toliki će i HM biti deo od GZ. Prema tome ostatak MK će onoliki deo od ostatka ZD koliki je ceo broj HK deo celog broja GD. A, opet, koliki KQ bude bio deo od GD, toliki će i EL biti deo od GZ; a kako je GD veće od GZ, biće Q K veće od EL. Konstruišimo KN jednako EL. Onda koliki KQ bude bio deo od GD, toliki će i KN biti deo od GZ. Prema tome će i ostatak NQ biti onoliki deo od ostatka ZD, koliki je ceo broj KQ deo celog broja GD. A dokazali smo da je i ostatak MK onoliki deo od ostatka ZD, koliki je ceo broj HK deo celog broja GD. Te prema tome je i zbir MK i NQ onoliki deo od DZ, koliki je ceo broj QH deo celog broja GD. No zbir MK i NQ jednak je EB, a QH je jednako BA. Na ovaj način, ostatak EB čini iste delove od ostatka ZD kao i ceo broj AB od celog broja GD. A to je trebalo dokazati.