Ako je jedan broj isti deo drugog broja kakav je i umanjilac prvog broja deo umanjioca drugog broja, onda je i ostatak prvog broja isti deo ostatka drugog broja.

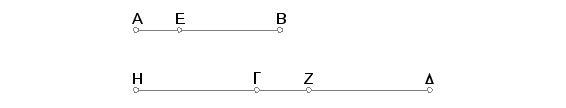
Neka je broj AB isti deo broja GD kakav je umanjilac AE deo umanjioca GZ. Tvrdim, da je i ostatak EB isti deo ostatka ZD kakav je i ceo broj AB celog broja GD.
Zaista, neka je EB isti deo od GH kakav je i AE deo od GZ, biće i AE isti deo od GZ kakav i AB od HZ. Ali se pretpostavlja da je AB onoliki deo od GD koliki je AE deo od GZ. Znači da je AB onoliki deo od HZ, koliki je isti taj broj deo od GD. Prema tome je broj HZ jednak broju GD. Oduzmimo zajednički broj GZ; tada je ostatak HG jednak ostatku ZD. A kako je AE isti deo od GZ, kao i EB od HG, a HG je jednak ZD, biće AE onoliki deo od GZ, koliki je EB deo od ZD. Ali koliki AE bude bio deo od GZ toliki će i AB biti deo od GD. Na ovaj način je ostatak EB onoliki deo od ostatka ZD, koliki je ceo broj AB deo celog broja GD. A to je trebalo dokazati.