Ako jedan broj čini delove drugog broja i neki drugi broj čini iste delove nekog drugog broja, onda i zbir prvih brojeva čini iste delove zbira drugih brojeva kao pojedini broj od pojedinog.

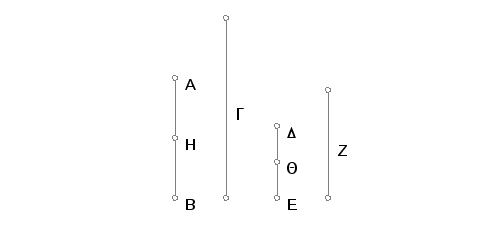
Neka broj AB čini delove broja G i sa druge strane, DE čini iste delove broja Z kao i AB od G. Tvrdim da i zbir AB i DE čini iste delove od zbira G i Z kao i AB od G.
Zaista, pošto kolike delove AB čini od G tolike će delove činiti i DE delova od Z; a to znači da je u AB isto toliko delova od G koliko DE delova od Z. Podelimo AB na AH, HB, delove od G, a DE na DQ i QE delove od Z; tada će biti toliko delova AH, HB, koliko delova DQ, QE. I pošto koliki AH bude bio deo od G toliki će i DQ biti od Z, to će koliki AH bude bio deo od G, toliki deo i zbir AH i DQ biti od zbira G i Z. Iz istih razloga, koliki je deo HB od G, toliki je deo i zbir HB i QE od zbira G i Z. Prema tome koliki su delovi AB od G isto toliki su delovi zbir AB i DE od zbira G i Z. A to je trebalo dokazati.