5.
Ako jedan broj čini deo drugog broja i neki drugi broj čini isti deo nekog drugog broja, onda i zbir prvih brojeva čini isti deo zbira drugih brojeva, kao pojedini broj pojedinog.
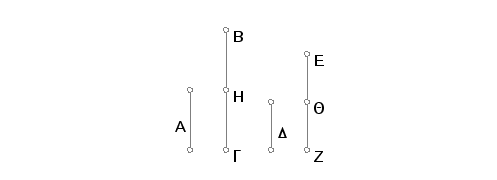
Neka je broj A deo broja BG, i neki drugi broj D isti deo, kao i A od BG, nekog drugog broja EZ. Tvrdim da je zbir A i D isti deo od zbira BG i EZ kao i A od BG.
Zaista, pošto koliki deo A bude bio od BG, toliki će deo i D biti od EZ, to će BG sadržati isto toliko puta A, koliko puta EZ sadrži D. Podelimo sad BG na delove BH, HG jednake A, a EZ na EQ, QZ jednake D. Tada je delova BH, HG isto toliko, koliko je delova EQ, QZ. I kako je BH jednako A, a EQ jednako D, biće i zbir BH i EQ jednak zbiru A i D. Iz istih razloga je i zbir HG i QZ jednak zbiru A i D. Prema tome koliko je u BG brojeva jednakih A, toliko je u zbiru brojeva BG i EZ zbirova brojeva A i D. Prema tome koliki je BG multiplum od A, isto toliki multiplum je zbir BG i EZ od zbira A i D. Na ovaj način, koliki je deo A od BG, isto toliki će deo biti zbir A i D od zbira BG i EZ. A to je trebalo dokazati.