4.
Svaki broj je ili deo ili delovi od svakog drugog broja, manji od većeg.
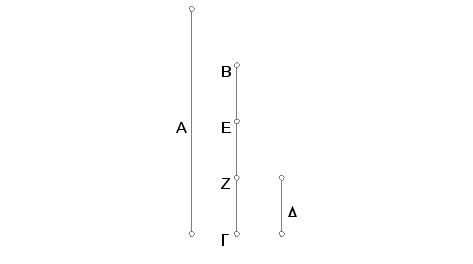
Neka su A i BG dva broja i BG je manji. Tvrdim da je BG ili deo ili delovi broja A.
Zaista, brojevi A i BG ili su međusobno prosti ili nisu. Neka su, prvo, brojevi A i BG međusobno prosti. Tada pri podeli BG na njegove jedinice, svaka od jedinica BG je deo broja A, a BG je deo broja A.
Neka sada brojevi A i BG nisu međusobno prosti. Tada je BG ili mera za A ili nije. Ako je BG mera za A, onda je BG deo od A. Ako nije, uzmimo najveću zajedničku meru D brojeva A i BG i podelimo BG na BE, EZ, ZG koji su jednaki D. Međutim kako D meri A, biće D deo od A. Ali svaki od brojeva BE, EZ, ZG jednak je D, te je prema tome svaki od BE, EZ, ZG deo od A. Prema tome je broj BG jednak delovima od A.
Na ovaj način, svaki broj je ili deo ili delovi od svakog drugog broja, manji od većeg.