33.
Za datu proizvoljnu množinu brojeva naći najmanje brojeve koji su u istim razmerama kao i dati.
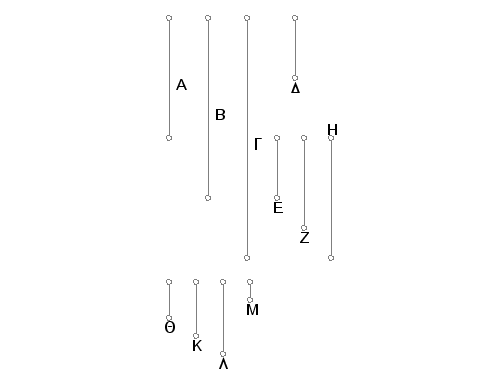
Neka su A, B, G dati brojevi u proizvoljnom broju. Naći najmanje brojeve koji su u istim razmerama sa datim brojevima A, B, G.
Zaista, brojevi A, B, G su ili uzajamno prosti ili nisu. Ako su brojevi A, B, G uzajamno prosti, oni su najmanji od onih koji stoje u istim razmerama sa njima.
Ako nisu, onda uzmimo najveću zajedničku meru D brojeva A, B, G. I neka se koliko puta D meri A, B, G, isto toliko jedinica nalaze u E, Z, H. Tada svaki od E, Z, H meri svaki od A, B, G prema broju jedinica u D. Prema tome E, Z, H mere isti broj puta brojeve A, B, G. Brojevi E, Z, H su u istim razmerama sa brojevima A, B, G. Tvrdim da su oni i najmanji. Zaista, ako E, Z, H nisu najmanji od brojeva koji su sa A, B, G u istim razmerama, onda postoje brojevi koji su sa A, B, G u istim razmerama, a koji su manji od E, Z, H. Neka su to brojevi Q, K, L. Tada Q meri broj A isti broj puta kao što i svaki od K, L meri brojeve B, G. Neka u M bude onoliko jedinica koliko se puta Q sadrži u A. Tada i svaki od brojeva K, L meri brojeve B, G prema broju jedinica u M. I pošto Q meri A prema broju jedinica u M, to i M meri A prema broju jedinica u Q. Iz istih razloga M meri svaki od brojeva B, G prema broju jedinca u svakom od brojeva kao K, L. Prema tome M meri brojeve A, B, G. I pošto Q meri A prema broju jedinica u M, to Q pomnoženo sa M proizvodi A. Iz istih razloga E pomnv zeno sa D proizvodi A. A tada je proizvod E, D jednak proizvodu Q, M, te je, prema tome, E prema Q kao M prema D. Međutim broj E je veći od broja Q, što znači da je i M veći broj od D i meri A, B, G. A to je nemoguće, pošto je D najveća zajednička mera brojeva A, B, G. Prema tome ne postoje brojevi koji su u istoj razmeri sa brojevima A, B, G, i koji su manji od brojeva E, Z, H. Na ovaj način brojevi E, Z, H su najmanji od brojeva koji u istoj razmeri sa brojevima A, B, G. A to je trebalo dokazati.