3.
Za tri data broja koji nisu međusobno prosti naći njihovu najveću zajedničku meru.
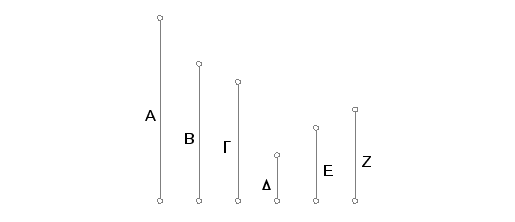
Neka su data tri broja A, B, G koji nisu međusobno prosti. Treba za A, B, G, naći najveću zajedničku meru.
Uzmimo najveću zajedničku meru D za dva broja A i B, ta mera ili je mera i broja G ili nije. Neka prvo ona bude mera. Ali ona je mera i brojeva A i B. Na taj način ona meri A, B, G, te je D zajednička mera za A, B, G. Tvrdim da je ona i najveća. Zaista, ako D nije najveća zajednička mera za A, B, G, onda brojeve A, B, G meri broj veći od D. Neka postoji takav broj i neka to bude E. Kako E meri A, B, G, meriće i A i B. Dakle meriće i njihovu najveću zajedničku meru. Ali najveća zajednička mera A i B je D. Prema tome E meri D, veći broj-manji, a to je nemoguće. Prema tome ne postoji broj veći od D koji bi merio brojeve A, B, G. Na taj način je D najveća zajednička mera brojeva A, B, G.
Neka sad D ne meri G. Prvo tvrdim da brojevi G i D neće biti međusobno prosti, meri ih neki broj. Broj koji meri brojeve A, B, G meri i brojeve A, B i njihovu najveću zajedničku meru D. Ali on meri i broj G. Prema tome za brojeve D, G postoji broj koji ih meri, brojevi D i G nisu prema tome međusobno prosti. Uzmimo njihovu najveću zajedničku meru E. Pošto E meri D, a D meri A i B, to E meri A i B. Ali E meri i G. Na ovaj način E meri A, B, G, te je E zajednička mera za A, B, G. Tvrdim da je ona i najveća. Zaista, ako E nije najveća zajednička mera A, B, G onda će brojeve A, B, G meriti neke broj veći od E. Neka takav broj postoji i neka to bude Z. Kako Z meri A, B, G, on meri i A, B. A kako je najveća zajednička mera A i B broj D, onda Z meri i D. Ali Z meri i broj G, prema tome Z meri D i G, i najveću zajedničku meru brojeva D i G. A kako je E najveća zajednička mera brojeva D, G, to Z meri E, veći broj manji, a to je nemoguće. Prema tome ne postoji za brojeve A, B, G broj veći od E koji meri te brojeve. Na ovaj način E je najveća zajednička mera za A, B, G. A to je trebalo dokazati.