27.

Ako su dva broja uzajamno prosti i svaki pomnoži sam sebe, onda su i njihovi proizvodi uzajamno prosti; i ako se prvobitni brojevi pomnože dobijenim proizvodima, onda su i novi proizvodi uzajamno prosti (a to isto se dobija i dalje).

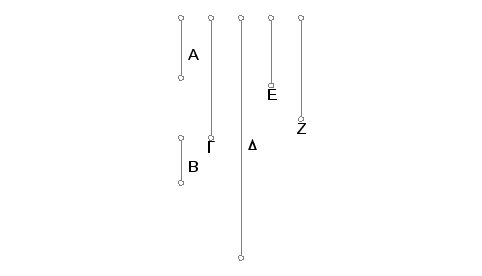
Neka su A i B dva uzajamno prosta broja, i neka broj A pomnožen sam sobom proizvodi G, a pomnožen brojem G proizvodi broj D, pa broj B pomnožen sam sobom proizvodi E, a pomnožen brojem E prooizvodi Z. Tvrdim da su brojevi G, E i D, Z uzajamno prosti.
Zaista, pošto su A i B uzajamno prosti, a broj pomnožen sam sobom proizvodi G, onda su i G, B uzajamno prosti. Pošto su sad G, B uzajamno prosti, a B pomnožen sam sobom proizvodi E, onda su i G, E uzajamno prosti. Dalje, pošto su A i B uzajamno prosti, a broj B pomnožen sam sobom dalje E, onda su i brojevi A, E uzajamno prosti. Pošto su sad dva broja A i G oba uzajamno prosta prema svakom od brojeva B, E biće i proizvod od A i G uzajamno prost sa proizvodom od B i E. A kako je proizvod od A i G broj D, a proizvod od B i E je broj Z, onda su brojevi D i Z uzajamno prost. A to je trebalo dokazati.