21.
Međusobno prosti brojevi su najmanji od onih koji su sa njima u istoj razmeri.
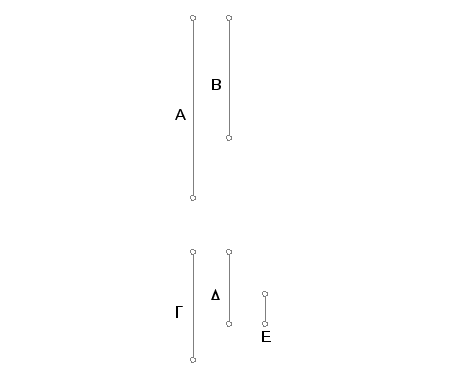
Neka su A i B međusobno prosti brojevi. Tvrdim da su oni i najmanji od onih koji su sa njima u istoj razmeri.
Ako nije tako, onda postoje brojevi manji od A i B koji su sa A i B u istoj razmeri. Neka to budu brojevi G i D. Pošto tada najmanji brojevi mere isti broj puta brojeve koji su sa njima u istoj razmeri, i to veći broj meri veći i manji broj-manji, predhodni meri predhodni i naredni-naredni, znači da G meri isti broj puta A kao što D meri B. A G meri onoliko puta koliko je jedinica u E. Pa prema tome i D meri B onoliko puta koliko je jedinica u E. I kako G meri A prema broju jedinica u E, to i E meri A prema broju jedinica u G. Iz istih razloga i E meri B prema broju jedinica u D. Prema tome E meri brojeve A i B koji su međusobno prosti, a to je nemoguće. Dakle, ne postoje brojevi manji od A i B koji su istoj razmeri sa njima. Na ovaj način brojevi A i B su najmanji od onih koji su u istoj razmeri sa njima. A to je trebalo dokazati.