20.

Najmanji među brojevima koji su istoj razmeri mere ostale isti broj puta i to veći meri veće i manji manje.

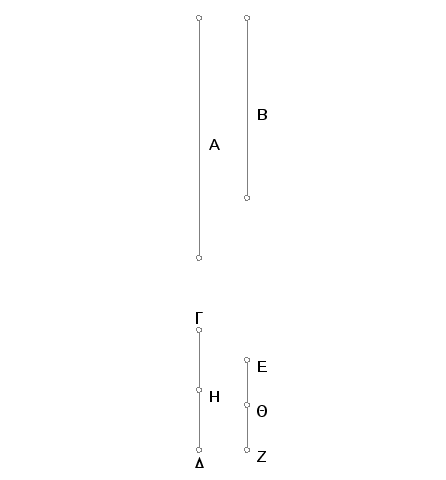
Neka su GD i EZ najmanji brojevi od brojeva A i B, koji stoje u istoj razmeri. Tvrdim da broj GD meri broj A, a broj EZ broj B isti broj puta.
Broj GD ne čini delove broja A. No, ako je to moguće, uzmimo da čini. Tada i EZ čini iste delove od B kao i GD od A. Prema tome koliko je u GD delova od A, isto toliko će biti i u EZ delova B. Podelimo GD na delove GH, i HD jednake delovima A i EZ na delove EQ i QZ jednake delovima B. Tada je broj podelaka GH, HD jednak broju podelaka EQ, QZ. I pošto su delovi GH i HD međusobno jednaki brojevi, a EQ i QZ isto tako međusobno jednaki brojevi, i broj podelaka GH, HD jednak je broju podelaka EQ, QZ, biće GH prema EQ kao HD prema QZ. A kako je jedan od predhodnih prema jednom od narednih kao zbir svih predhodnih prema zbiru svih narednih, to je GH prema EQ kao GD prema EZ. Na ovaj način GH i EQ se nalaze u istoj razmeri kao i GD i EZ i prvi su manji od drugih. A to je nemoguće, jer se pretpostavlja da su GD i EZ najmanji od svih brojeva koji se nalaze u istoj razmeri sa njima. Prema tome broj GD ne čini delove broja A. Taj broj je deo. I EZ je isti deo od B kao što je GD deo od A. Na ovaj način broj GD meri broj A isto onoliko puta, koliko i broj EZ meri broj B. A to je trebalo dokazati.