10.

Ako jedan broj čini delove drugog broja, a treći broj čini iste delove četvrtog broja, onda će posle permutacije, delovi ili deo prvog od trećeg broj biti jednki delovima ili delu drugog od četvrtog broja.

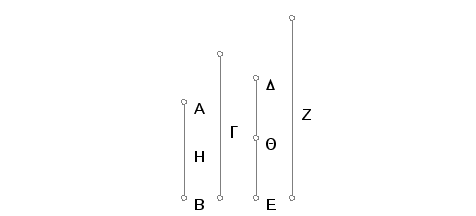
Neka broj AB čini delove broja G, drugi neki broj DE iste delove broja Z. Tvrdim da će posle permutacije, AB sačinjavati od DE iste delove ili isti deo, kao što će G sačinjvati delove ili deo od Z.
Zista, koliko delova AB čini od G, toliko delova čini i DE od Z, a to znači koliko delova od G sadrži AB, toliko delova od Z sadrži DE. Podelimo AB na delove AH, HB jednake delovima broja G, a DE na delove DQ, QE jednake delovima broja Z. Broj podelaka AH, HB biće jednak broju podelaka DQ, QE. I pošto koliki deo AH čini od G, isto toliki deo DQ čini od Z, to će, posle permutacije, i G činiti onoliki deo ili delove od Z koliki deo ili delove bude činio HB od QE. Prema tome, [koliki deo ili delove AH čini od DQ, toliki deo ili delove čini i HB od QE. Znači koliki deo ili delove AH čini od DQ, toliki deo ili delove čini AB od DE, no dokazano je da koliki deo ili delove AH čini od DQ, toliki deo ili delove G čini od Z, i] koliko delova ili deo AB čini od DE, toliko delova ili deo čini i G od Z. A to je trebalo dokazati.