1.
Ako su data dva nejednaka broja pa pri uzastopnom oduzimanju manjeg od većeg ostatak ne biva mera predhodnog, koji smo oduzimali, dok taj ostatak ne postane jednak jedinici, ta su dva broja međusobno prosti.
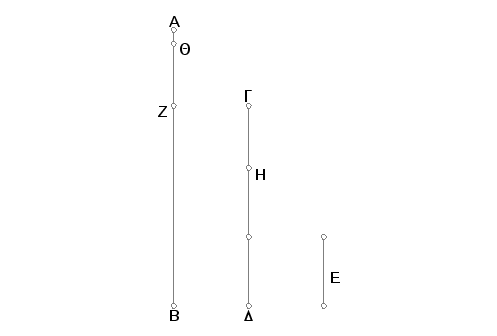
Neka za dva data broja AB i GD pri uzastopnom oduzimanju manjeg od većeg ostatak ne biva mera predhodnog, koji smo oduzimali, dok taj ostatak ne postane jednak jedinici. Tvrdim da su brojevi AB i GD međusobno prosti, tj. zajednička mera brojeva AB i GD je samo jedinica.
Zaista, ako AB i GD ne bi bili međusobno prosti, onda bi njihova zajednička mera bila neki broj. Neka ih, dakle, meri neki broj i neka to bude E. Neka DG pri merenju BA bude BZ i od AB ostavi još ZA, manji broj od DG; ZA pri merenju DG ostavi HG, manji broj od ZA, a HG pri merenju ZA ostavi QA koji je jednak jedinici.
Kako sad broj E meri broj GD, a BZ je jednak broju GD, to će E meriti i BZ; ali E i ceo broj AB, što znači da će E meriti i ostatak AZ. Međutim, AZ meri DH, znači E meri i DH. Ali E meri i ceo broj DG, znači on će meriti i ostatak GH. Dalje, GH meri ZQ, te prema tome E meri i ZQ. Ali E meri i ceo broj ZA, te tako E meri i ostatak, jedinicu. To bi značilo da postoji broj koji meri jedinicu, a to je nemoguće. Prema tome ne postoji nikakav broj koji bi merio brojeve AB i GD. Brojevi AB i GD su na taj način međusobno prosti. A to je trebalo dokazati.