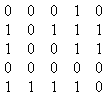
BSO,
a radi jednostavnosti kôda, smatrajmo da su u matrici
sussedstva na dijagonali nule. JASNO
je da super star ima sve 1ce u svojoj koloni (osim za i=j) i sve 0 u
svojoj vrsti .
1. Nema garancije da će neka strategija dati tačno rešenje (ono može biti i samo približno)
2. Dobijeni algoritam ne mora biti ni efikasan
3. Ove strategije su se pokazale uspešne za mnoge probleme, pa je to razlog zašto se najčešće koriste u rešavanju novih problema
1. Među n osoba
superstar
je osoba koja ne
poznaje nikoga, a koju svi ostali poznaju.
Problem:
Identifikovati superstar-a (ako postoji) postavljajući pitanja
oblika "Izvinite, da li poznajete onu osobu?" sa ciljem da
se minimizira ukupan broj pitanja. Pretpostaviti da:
odgovori su u formi da/ne
svi odgovori su tačni
superstar će dati odgovor
Slučaj n=2 je jednostavan. (do 2 pitanja)
Rešenje br. 1
Kako ima ukupno n(n-1)/2 parova osoba, onda u najgorem slučaju se može postaviti n(n-1) pitanja (ako se pitanja postavljaju bez neke mudre strategije za svaki par).
Rešenje br. 2
Posmatrajmo razliku problema dimenzije n-1 (sa n-1 osobom) i problema dimenzije n. Neka je induktivna hipoteza (IH) da znamo da pronađemo superstar-a među prvih n-1 osoba. Kako broj superstar-a nije veći od jedan, onda postoje tri mogućnosti:
superstar je međi prvih n-1 osoba
superstar je n-ta osoba
ne postoji superstar
Slučaj 1 je najjednostavniji: proveri se samo da li n-ta osoba ne poznaje superstar-a, tj. da li je tačno da superstar ne poznaje ni n-tu osobu
Slučajevi 2 i 3 su teži, jer da bi se proverilo da li je n-ta osoba superstar, ukupan broj potrebnih pitanja je 2*(n-1) /*bitno je da n-1 osoba poznaje superstar-a, kao i da superstar ne poznaje ostale osobe*/. Dakle, ako je u n-tom koraku broj potrebnih pitanja 2*(n-1), onda će ukupan broj pitanja n*(n-1), a taj slučaj je odbačen još u rešenju 1.
IDEJA:posmatranje problema u obrnutom smeru i pokušati identifikovati osobu koja nije superstar (a broj onih koji nisu superstar je mnogo veći).
Dakle, eliminišimo neku osobu koja nije super-star iz problema i time se dimenzija problema sa n smanjuje na n-1. Nije bitno ko se eliminiše. Na primer: ako osobu A pitamo da li poznaje osobu B, onda:
ako poznaje osobu B, eliminiše se osoba A
u suprotnom, eliminiše se osoba B, jer nije superstar
Uočimo da je bilo dovoljno samo jedno pitanje za eliminaciju jedne osobe.
Podsetimo se već spomenute tri mogućnosti pri prelasku sa n-1 na n i uočimo razliku u tome da se n-ta osoba ne bira proizvoljno.
Eliminacijom osobe A li osobe B, dimenzija problema je smanjena i slučaj 2. (superstar je n-ta osoba) se ne mora razmatrati, jer eliminisana osoba ne može biti superstar.
Ako se desi slučaj 3, tj. ako nema superstar-a među prvih n-1 osoba, onda ga nema ni među n osoba.
Ako se desi slučaj 1, tj. ako postoji superstar među prvih n-1 osoba, onda je potrebno još dva pitanja da li je on superstar za kompletan skup, a ako nije, onda ne postoji superstar za skup.
Realizacija
Algoritam se deli u dve faze. U prvoj fazi se vrši eliminacija svih osoba sem jedne-kandidata za superstar-a, a potom se u drugoj fazi testira da li kandidat jeste superstar. Podsetite se algoritma za traženje ponora grafa!!!
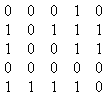
BSO,
a radi jednostavnosti kôda, smatrajmo da su u matrici
sussedstva na dijagonali nule. JASNO
je da super star ima sve 1ce u svojoj koloni (osim za i=j) i sve 0 u
svojoj vrsti .
Složenost
U najgorem slučaju postavlja se najviše 3*(n-1) pitanja. (U prvoj fazi se postavi n-1 pitanja radi eliminacije n-1 osobe, a u drugoj fazi se postavlja ne više od 2(n-1) pitanja). Dimenzija problema jeste n, ali veličina ulaza je n(n-1) /*ulaz je matrica odgovora*/, a ovaj algoritam pregleda najviše O(n) elemenata matrice, iako je ulaz reda n2.
pseudo-jezik:
Algoritam
Superstar(Poznaju)
input: Poznaju
/* n*n matrica
čiji elementi su:
Poznaju[i][j]=1, ako osoba i poznaje osobu
j
Poznaju[i][j]=0, ako osoba i ne poznaje osobu j , gde
i,j=1..n
*/
output: Superstar /* 0,
ako ne postoji ili 1, ako postoji */
{
i=1; /*osoba A*/
j=2; /*osoba B*/
Sled=3; /*sledeci koji ce se proveravati*/
/*prva faza*/
while (Sled <=n+1)
{
if
(Poznaju[i][j]==1)
i=Sled; /*i
nije superstar, eliminacija*/
else
j=Sled; /*j nije superstar, eliminacija*/
Sled=Sled+1;
}
/*nakon izlaska iz petlje
ili je i=n+1 ili je j=n+1 */
if (i==n+1)
kandidat=j
else
kandidat=i
/*druga
faza*/
Jeste=1; /*1 ako kandidat jeste superstar*/
k=1;
/*osoba iz skupa*/
while ( (Jeste==1) && (k <=n) ) /*
&& - log. operat. konjukcije */
{
if
(Poznaju[kandidat,k]==1)
Jeste=0;
/*kandidat nije superstar*/
if
(Poznaju[k,kandidat]==0 && k!=kandidat)
Jeste=0; /*kandidat nije superstar*/
k=k+1;
} /*while iz druge faze*/
/*odluka o rezultatu*/ if
(Jeste==1) Superstar=kandidat
else Superstar=0; /*nema
superstar-a*/
output superstar
}
2.Implementirati algoritam tipa podeli-pa-vladaj koji određuje najveći i drugi najveci elemenat niza A velicine n. Odrediti vremensku slozenost algoritma.
IDEJA i podsecanje:
Podeliti niz na dve polovine, naci dva najveća elementa u svakoj od polovina i na osnovu njih odrediti najveci i drugi najveci elemenat niza.
3.Implementirati algoritam koji odredjuje broj čvorova u binarnom stablu. Ako binarno stablo ima n cvorova odrediti vremensku i prostornu slozenost algoritma.
4. Primer
neifikasne primene strategije PODELI-PA_VLADAJ: Rekurzija za
računanje clana Fibonacijevog niza: F(0) = F(1) = 1 ; F(n) =
F(n-2) + F(n-1) , n > 2
Strategija
podeli-pa-vladaj daje rekurzivnu funkciju za određivanje
Fibonaccijevih brojeva:
int fib( int n ) {
if ( n < 2 ) return
1; else return fib(n-1) + fib(n-2);
}
Složenost algoritma:
označimo s T(n) vreme potrebno za izračunavanje Fn.
Tada važi: T(n) = T(n-1)
+ T(n-2) , početni uslov: T(1) = T(2) = c
Karakteristična
j-na ove rekurzije: x2
– x - 1 = 0 ,
koreni su x1,2=
(1 ± √5)/2
Opste rešenje
rekurzije: Fn = C1 {(1+√5)/2}n
+ C2 {(1-√5)/2}n
Konstante C1 i C2 se
odrede iz početnih uslova: C1 = - C2 = 1/√5, te je
rešenje:
F(n) = 1/√5
{(1+√5)/2}n
- 1/√5
{(1-√5)/2}n
T(n) = O({(1+√5)/2}n)
= O(1.618n)
Dakle, vreme izvršavanja
raste eksponencijalno s veličinom ulaza
ZNATE
LI EFIKASNIJI ALGORITAM ZA RACUNANJE Fn?
Koja
bi bila vremenska i prostorna slozenost tog algoritma?
5. Dat je hip sa n elemenata tako da najveći element je u korenu. Dat je i realan broj x. Konstruisati algoritam koji samo utvrđuje da li je k-ti najveći element hipa manji ili jednak od x. Nije nužno odrediti k-ti najveći element hipa, nego samo ustanoviti njegov odnos sa x. Vremenska složenost algoritma mora da (nezavisno od veličine hipa) bude O(k). Dozvoljeno je koristiti memorijski prostor veličine O(k) (u slučaju da se koristi rekurzija, dozvoljeno je koristiti memorijski prostor veličine O(k) za pamćenje rekurzivnih poziva, tj. za stek).
k-ti najveći element hipa veći od x <=> postoji k
elemenata hipa koji su veći od x, k >= 0
broj=0; /*
promenljiva koja cuva broj elemenata vecih od x; ova promenljiva mora
ziveti, tj. cuvati vrednost izmedju rekurzivnih
poziva,
te je staticka ili globalna ili ...*/
odgovor=NE; /*
odgovor da li je k-ti najveći element hipa manji ili
jednak od x */
Algoritiam Utvrdi
(Hip H sa korenom v,
x, k)
ulaz: H, k, x
izlaz: odgovor DA/NE
{
if (!v) return
ODGOVOR;
if (v->vrednost > x) broj++;
if (broj > k) return (odgovor==DA);
Utvrdi(H sa korenom
v->prviSin, x,k);
Utvrdi(H sa korenom v->drugiSin,
x,k);
}
Bez obzira na veličinu hipa, broj rekurzivnih poziva f-je Utvrdi je O(k), jer algoritam se rekurzivno spušta niz hip H i uvećava promenljivu broj sve dok se ne prođe ceo hip H ili se ne izbroji k elemenata. Za pamćenje rekurzivnih poziva potrebno je koristiti stek, tj. memorijski prostor O(k)
6. Neka su A i B dva skupa od n elemenata, pri čemu se A čuva u računaru P, a B u računaru Q. Računari mogu da komuniciraju razmenjujuci poruke, amogu i da izvrše bilo kakvo lokalno izračunavanje. Konstruisati algoritam koji određuje n-ti najmanji element skupa A U B (tj. medijanu). Može se, zbog jednostavnosti, pretpostaviti da je A∩B = {}. Cilj je minimizirati broj poruka, pri čemu poruka može da sadrđi jedan element ili jedan ceo broj. Koliki je broj poruka potreban u najgorem slučaju?
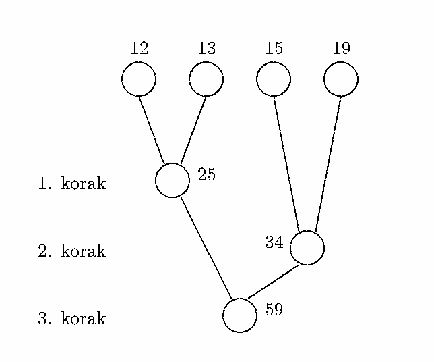
7. Primer efikasne primene pohlepnog algoritma: Hafmanovo kôdiranje
8. Primer efikasne primene pohlepnog algoritma:
Trgovac treba da vrati mušteriji kusur od 62 dinara, na raspolaganju su mu novčanice od 50, 20, 10, 5 i 1 dinara. Instinktivno će većina ljudi vratiti 1x50, 1x10 i 2x1 dinar. Takav algoritam vraća tačan iznos uz najkraću moguću listu novčanica
Algoritam: izabere se najveća novčanica koja ne prelazi ukupnu sumu (50 dinara), stavlja se na listu za vraćanje, oduzme se vraćena vrednost od ukupne kako bi se izračunao ostatak za vraćanje (12 dinara), zatim se bira sledeća novčanica koja ne prelazi ostatak koji treba vratiti (10 dinara), dodaje se na listu za vraćanje i računa novi ostatak za vraćanje (2 dinara) itd, sve dok se ne vrati tačan iznos
Dakle strategija pohlepnog pristupa je u konkretnom primeru sa 62 dinara dovela do najefikasnijeg rešenja problema vraćanja novca i to zahvaljujući specijalnim svojstvima raspoloživih novčanica!!!
9.
Implementirati pohlepni algoritam za vracanje kusura za dati iznos n>=0 sa monetamama iz skupa {1, 5, 10, 20, 40, 50, 200, 500}. Pokazite da pohlepni algoritam nije optimalan za ovaj skup novcica.
IDEJA kao u prethodnom zadatku:
Neka u algoritmu KUSUR(n) je:
broj novcica od 1 dinara je g1
broj novcica od 5 dinara je g2
broj novcica od 10 dinara je g3
broj novcica od 20 dinara je g4
broj novcica od 40 dinara je g5
broj novcica od 50 dinara je g6
broj novcica od 200 dinara je g7
broj novcica od 500 dinara je g8
Pseudo-kod je implementacija ideje iz prethodnog zadatka:
KUSUR(n)
g1 = 0; g2 = 0; g3 = 0; g4 = 0; g5 = 0;
g6 = 0; g7 = 0; g8 = 0;
while (n >= 500 ) {g8 = g8 + 1; n = n − 500;}
while (n >=200 ) { g7 = g7 + 1; n = n − 200;}
while (n >= 50) { g6 = g6 + 1; n = n − 50;}
while (n >= 40) { g5 = g5 + 1; n = n − 40;}
while (n >= 20) { g4 = g4 + 1; n = n − 20;}
while {n >= 10) { g3 = g3 + 1; n = n − 10;}
while (n >=5) { g2 = g2 + 1; n = n − 5;}
while (n >= 1) { g1 = g1 + 1; n = n − 1;}
OUTPUT: g1, g2, g3, g4, g5, g6, g7, g8 ;
Jasno je da vreme izvrsavanja gore navedenog algoritma KUSUR(n) jeste O(g1 + g2 + g3 +g4 + g5 + g6 + g7 + g8 ).
Pohlepni algoritam nije optimalan za ovaj skup novčića, jer kusur od 80 dinara bi vratio u tri monete 50, 20 i 10, a optimalno bi bilo da se vrate samo dve monete od 40 dinara.
10.
Potrebno je n sortiranih listi duzine w1, w2, …, wn spojiti u jednu veliku sortiranu listu. Spajanje se obavlja u n-1 koraka tako da se u svakom koraku spoje dve odabrane liste algoritmom merge (dat kao crna kutija). Traži se optimalni plan sažimanja uz takav odabir listi u pojedinom koraku kako bi se postigao najmanji ukupni broj operacija.
RESENJE:
Optimalni plan spajanja se može odrediti pohlepnim pristupom i može se pokazati da ga konstruise zapravo Huffmanov algoritam: u svakom koraku spajanja treba odabrati dve najkraće liste (drugim rečima svaki korak se izvodi tako da imamo najmanje posla u tom koraku)
11. Moze se smatrati da je zadata vrednost kapacitet ranca c, da wi su težine predmeta koje se mogu staviti u ranac, pi vrednosti tih predmeta i xi označava koji se deo i-tog predmeta stavlja u ranac. Problem se sastoji u odredjivanju predmeta koje treba staviti u ranac tako da ukupna tezina ∑i=1...n wi*xi ne bude veca od c, a da ukupna vrednost ∑i=1...n pi*xi bude maksimalna. Predmeti se mogu rezati (oznaka xi)
ILI
Zadat je prirodan broj n i pozitivni realni brojevi c, wi i pi(i=1,2,…,n). Traže se realni brojevi xi(i=1,2,…,n) takvi da je
∑i=1...n pi*xi maksimalna uz ograničenja ∑i=1...n wi*xi <= c, 0<=xi<=1 (i=1,2,…,n).
TEST PRIMER:
n=3, wi=(2,3,4), pi=(1,7,8), c=6.
RESENJE TEST primera
Algoritam stavlja u ranac celi drugi predmet (ZASTO? Jer se od njega najvise profitira (uocite odnos pi / wi )),
te ga popunjava s 3/4 trećeg predmeta, te je rešenje xi=(0,1,3/4) i maksimalna vrednost u rancu je 13.
12. Egipatski razlomci. Svaki pozitivan broj se može prikazati kao zbir različitih pozitivnih razlomaka sa jediničnim brojiocima. Na primer,
![]()
Uzmite u obzir da jedan razlomak može da ima više egipatskih prikazivanja. Opišite efikasan pohlepni algoritam koji za dati razlomak određuje egipatsko prikazivanje razlomka.
P1. Za zadate cele brojeve a0, aq,...,an-1 pronaći maksimalnu vrednost sume ∑k=i..j ak, gde 0<=i<=n-1,0<=j<=n-1 i u slučaju nepraznog podniza i <= j smatrati da maksimalna vrednost sume elemenata podniza niza a je nula, ako su svi članovi podniza negativni.
Test-primer:
|
n |
niz |
max suma podniza |
podniz |
|
3 |
2, 4, 6 |
12 |
2,4,6 |
|
6 |
1, -3, 4,-2, -1, 6 |
7 |
4,-2, -1, 6 |
|
11 |
1, 2, 3, 4, -100, 20, -5, -6, 10, 8, -10 |
27 |
20, -5, -6, 10, 8 |
Pre algoritma, razmotrimo gore navedenu napomenu, odnosno mogućnost pojave praznog podniza.
U slučaju da su na ulazu svi brojevi negativni, izlaz će biti 0 (po formulaciji problema). Iako bi izlaz mogao biti negativni broj najmanje aposolutne vrednosti. Razlog leži u situaciji pojave praznog podniza(sa 0 elemenata), koji jeste podniz i čija suma jeste 0. Kako je prazni podniz niz sa uzastopnim članovima, jasno je da je njegova suma kandidat za rešenje, te tako uvek postoji podniz uzastopnih elemenata čija suma je 0.
Formulisani problem je interesantan za diskusiju, jer postoji mnogo algoritama koji ga rešavaju, ali perfomanse tih algoritama drastično variraju.
Slede četiri algoritma koji rešavaju problem
brute force algoritam reda O(n3)
poboljšani algoritam reda O(n2)
algoritam reda O(n)
divide-and-conquer algoritam reda O(n log n)
Algoritam grube sile (a,n)
|
1 |
input: a, n |
|
|
2 |
output: maxSum |
|
|
3 |
{ |
|
|
4 |
/*inicijalizacije*/ |
|
|
5 |
|
maxSum=0; |
|
6 |
|
/* sekStart i sekEnd su početak i završetak trenutne sekvence-kandidata za rešenje*/ |
|
7 |
|
sekStart=0; |
|
8 |
|
sekEnd=-1; |
|
9 |
|
for (i=0; i < n; i++) |
|
10 |
|
for (j=i;j <n; j++) |
|
11 |
|
{ |
|
12 |
|
tekSum=0; /* suma tekuce sekvence*/ |
|
13 |
|
|
|
14 |
|
for (k=i; k <= j; k++) |
|
15 |
|
tekSum += a[k]; /*formiranje sume tekuce sekvence*/ |
|
16 |
|
|
|
17 |
|
if (tekSum > maxSum) |
|
18 |
|
{ |
|
19 |
|
maxSum=tekSum; |
|
20 |
|
sekStart=i; /*indeks pocetka sekvence-kandidata za resenje*/ |
|
21 |
|
sekEnd=j; /*zavrsetak sekvence-kandidata za resenje*/ |
|
22 |
|
} |
|
23 |
|
} |
|
24 |
} |
|
Na vreme
izvršavanja algoritma dominatno utiče unutrašnji
for ciklus (14,15).
Postoje 4 naredbe:
inicijalizacija k=i
test k <= j
sabiranje u 15
inkrementacija k++
Broj
ponavljanja fragmenta 15 dominira među ova četiri izraza.
Zašto?
Dakle, potrebno je izračunati ukupan broj
izvršavanja fragmenta 15 u čitavom algoritmu.
Broj ponavljanja fragmenta 15 jednak je broju uređenih
trojki (i,j,k)
za
koje važi 0 <= i <= k <= j < n, jer indeks i
prolazi
čitav niz, dok j
prolazi
vrednosti od indeksa i
do
indeksa poslednjeg člana niza, a k
ima
vrednosti između [i,
j].
Ukupan broj tih trojki je n(n+1)(n+2)/6 tj. O(n3).
Zašto?
Može li
se ukloniti petlja 14 i time poboljšati algoritam?
Može, jer a[i]
+ a[i+1] +...+ a[j ]= (a[i] + a[i+1] +...+ a[j-1] ) + a[j] = A[j-1]
+ a[j], tj. odbaciće se redundantnost ako se na već
izračunatu sumu A[j-1] doda a[j]. Zato
algoritam kvadratne složenosti glasi:
====================================================================
Algoritam PoboljsaniMaxSumTest2 (a,n)
1 input: a, n
2 output: maxSum
3 /* seqStart , seqEnd reprezentuju trenutnu sekvencu kandidata */
4
5 {
6 maxSum = 0;
7 seqStart = 0;
8 seqEnd = -1;
9
10
11
12 for( i = 0; i < n; i++ )
13 {
14 tekSum = 0;
15 for( j = i; j < n; j++ )
16 {
17 tekSum += a[ j ];
18
19 if( tekSum > maxSum )
20 {
21 maxSum = tekSum;
22 seqStart = i;
23 seqEnd = j;
24 }
25 }
26 }
27
28
29 }
30
U ovom algoritmu spoljašnji for ciklus se prolazi n puta, unutar kog je ugnježden for ciklus koji se prolazi potencijalno n puta unutar kog su 1-koracne naredbe dodele, sabiranja i poređenja, te oba for ciklusa imaju potencijalno n*n iteracija sa 1-koracnim operacijam =>: vremenska složenost je O(n2).
Može li se ukloniti petlja 15 i time poboljšati algoritam?
Može, jer i
algoritam broj 2 ima tzv. iscrpno pretraživanje svih mogućih
rešenja, tj. isprobavanje svih mogućih podnizova,
a
razlika algoritma 2 i algoritma 1 je što se kod algoritma 2
provera svakog uzastopnog podniza obavi za O(1) vreme, a kod
algoritma 1 za O(n) vreme.
Međutim broj mogućih
podnizova je O(n2), te poboljšanje algoritam se
može postići samo ako se nađe način da se neki
podnizovi eliminišu kao kandidati i da se ne vrši
izračunavanje njihovih suma i poređenje sa tekućim
maksimumom. Ali, to je tema algoritma 3.
===========================================================
Ideja
algoritma 3
OZNAKE:
Neka A[i,j] je podniz: a[i], a[i+1],...,a[j], neka S[i,j] =
a[i]+a[i+1] +...+ a[j]
Stav
1 Neka
A[i,j] je ma koja sekvenca za koju je S[i,j] < 0. Ako je q >
j, onda A[i,q] nije podniz maksimalne sume.
DOKAZ: Jasno je da:
S[i,q]=S[i,j] + S[j+1, q]. Kako je S[i,j] < 0, onda je S[i,q] <
S[j+1, q] => A[i,q] ne može biti podniz maksimalne sume.
Stav
2 Za
ma koje i, neka A[i,j] je prvi podniz za koji je S[i,j] < 0. Tada
za neko p takvo da i <= p <= j, p <= q važi da: ili A[p,q]
nije podniz maksimalne sume ili ima sumu jednaku sa do tada
pronađenim maksimuom.
DOKAZ:
Ako p==i, onda važi stav 1, tj. A[p,q] nije podniz maksimalne sume.
Inače,
S[i,q]=S[i,p-1]+S[p,q]
Kako j je najmanji indeks za koji S[i,j]
<0, onda je S[i, p-1] > = 0, pa je S[i,q] > S[p,q]
Ako
je q > j (videti SLIKA 1), onda po stavu 1 sledi A[i,q] nije
podniz maksimalne sume, te to nije ni A[p,q]. Inače (videti
SLIKA 2), podniz A[p,q] ima sumu jednaku bar već pronađenom
podnizu A[i,q].
KOJI JE SMISAO
UPOTREBE STAVA 1 i STAVA 2 u KONSTRUKCIJI ALGORITMA 4?
Po stavu
1 se u algoritmu 2 može izaći iz unutrašnje petlje ako
je tekSum < 0 i to se koristi u liniji 21 u algoritmu 3, dok stav
2 nam govori da u liniji 23 se može preći sa indeksa i na j+1.
U algoritmu 3, skaniranje podnizova se obavlja uvećanjem
indeksa j, tako da jedini for ciklus iterira najviše n puta,
a telo for ciklusa ima 1-koračne naredbe dodele, sabiranja uz
dva poređenja, te složenost je O(n).
SLIKA 1
|
i |
j |
j+1 |
|
q |
|
S[i,q] |
|
|||
|
> = 0 |
< = S[i,q] |
|
||
|
p-1 |
p |
|
||
SLIKA 2
|
i |
|
|
q |
j |
|
S[i,q] |
|
|||
|
> = 0 |
< = S[i,q] |
|
||
|
p-1 |
p |
|
||
Algoritam MaxSumTest3 (a,n)
/* algoritam reda O(n) */
/* seqStart, seqEnd reprezentuju trenutnu sekvencu kandidata */
1 input: a, n
2 output: maxSum
3
4 {
5 maxSum = 0;
6 thisSum = 0;
7 seqStart = 0;
8 seqEnd = -1;
9
10
11 for( i = 0, j = 0; j < n; j++ )
12 {
13 thisSum += a[ j ];
14
15 if( thisSum > maxSum )
16 {
17 maxSum = thisSum;
18 seqStart = i;
19 seqEnd = j;
20 }
21 else if( thisSum < 0 )
22 {
23 i = j + 1;
24 thisSum = 0;
25 }
26 }
27
28
29 }
=====================================================================
Algoritam MaxSumTest4 (a,n)
/* algoritam tipa "zavadi, pa vladaj" reda O(n log n) */
/* - Rekurzivni algoritam.
- Nalazi maximum sume u podnizu a[levo..desno].
- Ne radi se odrzavanje trenutne sekvence-kandidata za resenje */
1GlavniProgram
2 input: a, n output: maxSum
3 {
4 maxSum = n > 0 ? maxSumRec( a, 0, n - 1 ) : 0;
5 }
6 PoptProgram: int maxSumRec (a, left, right)
7 input: a, left, right //niz a, left, right = leva i desna granica podniza
8 output: max
9 { maxLeftBorderSum = 0, maxRightBorderSum = 0;
10 leftBorderSum = 0, rightBorderSum = 0;
11 center = ( left + right ) / 2;
12
13 if( left == right ) /* bazni slucaj */
14 return a[ left ] > 0 ? a[ left ] : 0;
15
16 /*rekurzivni pozivi po podnizovima*/
17 maxLeftSum = maxSumRec( a, left, center );
18 maxRightSum = maxSumRec( a, center + 1, right );
19
20 for( i = center; i >= left; i-- )
21 {
22 leftBorderSum += a[ i ];
23 if( leftBorderSum > maxLeftBorderSum )
24 maxLeftBorderSum = leftBorderSum;
25 }
26
27 for( i = center + 1; i <= right; i++ )
28 {
29 rightBorderSum += a[ i ];
30 if( rightBorderSum > maxRightBorderSum )
31 maxRightBorderSum = rightBorderSum;
32 }
33
34 max= max3( maxLeftSum, maxRightSum,
35 maxLeftBorderSum + maxRightBorderSum );
36 }
37
38 /* maximum tri broja */
39 Algoritam max3( a, b, c )
40 input: a,b,c
41 output: max 3 broja
42 {
43 return a > b ? a > c ? a : c : b > c ? b : c;
44 }
U
ovom algoritmu se koristi tehnika ZAVADI PA VLADAJ
(divide-and-conquer).
Taj metod dekompozicije obuhvata podelu ulaza na manje podskupove,
njihovu obradu rekurzivnim pozivom procedure (ZAVADI), i
objedinjavanje dobijenih rešenja (PA VLADAJ). Najčešće
se problem deli u potprobleme jednake veličine, tradicionalno
se onaj fragment algoritma koji ima bar dva rekurzivna poziva naziva
ZAVADI-PA-VLADAJ algoritam. Naravno, podproblemi (tj podskupovi
ulaza) se ne smeju preklapati, da bi se izbeglo prekomerni pozivi i
zračunavanja kakva npr. postoje u algoritmu koji rekurzijom
izračunava Fibonačijeve brojeve.
Ova tehnika se
koristi kod problema nalaženja konture skupa pravougaonika ili
sortiranja učešljavanjem ili quick sort-a.
Podniz maksimalne sume može:
kompletno pripadati levoj polovini niza ili
kompletno pripadati desnoj polovini niza ili
početi u levoj polovini niza, a zavrsiti u desnoj polovini niza
Zato je ideja sledeća
rekurzivno izračunati maksimalnu sumu podniza koji kompletno pripada levoj polovini niza (koraci 17)
rekurzivno izračunati maksimalnu sumu podniza koji kompletno pripada desnoj polovini niza (koraci 18)
u dva uzastopna ciklusa izračunati maksimalnu sumu podniza koji počinje u levoj polovini niza, a zavrsiti u desnoj polovini niza (koraci 20-32)
naći maksimum među te tri sume (koraci 34-35)
Kako
rekurzija zahteva i specificiranje baznog slučaja, tj. izlaz je
kada ulaz problema se sastoji samo od jednog elementa. U linijama
13-14 obezbeđen je izlaz iz rekurzije, jer kada left==right,
onda rezultat je ili nula ili vrednost jedinog, nenegativnog
elementa.
U linijam 17 i 18 izvode se rekurzivni pozivi, i ti
pozivi se uvek obavljaju nad potproblemima manje dimenzije od
polaznog, tj. tim pozivima se napreduje ka baznom slučaju, tj.
izlazu iz rekurzije.
Složenost
algoritma je O(n log n). Zašto?
Označimo sa T(n)
broj potrebnih vremenskih jedinica za rešavanje problema
maksimalne sume podniza u nizu dimenzije n.
Tada je
T(1)=1 (linije 13-14)
T(n)= 2 T(n/2) + O(n) ( 2 rekurzije u linijama 17-18, plus linije 20-32 za const*N operacija računaju maksimalnu sumu) )
Ova difrencna jednačina može da se reši tehnikom teleskopskih suma, ali i pozivom na master teoremu
Kako je u
algoritmu 4: a=2, b=2, a=b (tj. k=1), onda je T(n) = O (n log n)
ZADACI ZA VEZBU:
Za zadate cele brojeve a1, a2,...,an pronaći maksimalnu vrednost proizvoda ∏k=i..j ak, gde 1<=i<=n,1<=j<=n.
Ovo je varijanta prethodnog zadatka sa proizvodom umesto sume.